Geek Break: Calculating Elevation of Jet Transiting the Sun

Brandon Ghany on Flickr

After my last post about capturing a jet flying in front of the Sun, I saw this image Brandon Ghany posted on Flickr of a jet crossing in front of the Moon and what caught my attention is how much smaller the jet is than in my video. 

From Brandon's description, this jet was flying at about 12,500 feet. Clearly, the jet I caught was flying much lower. But how low? I was curious enough to try figuring it out. 

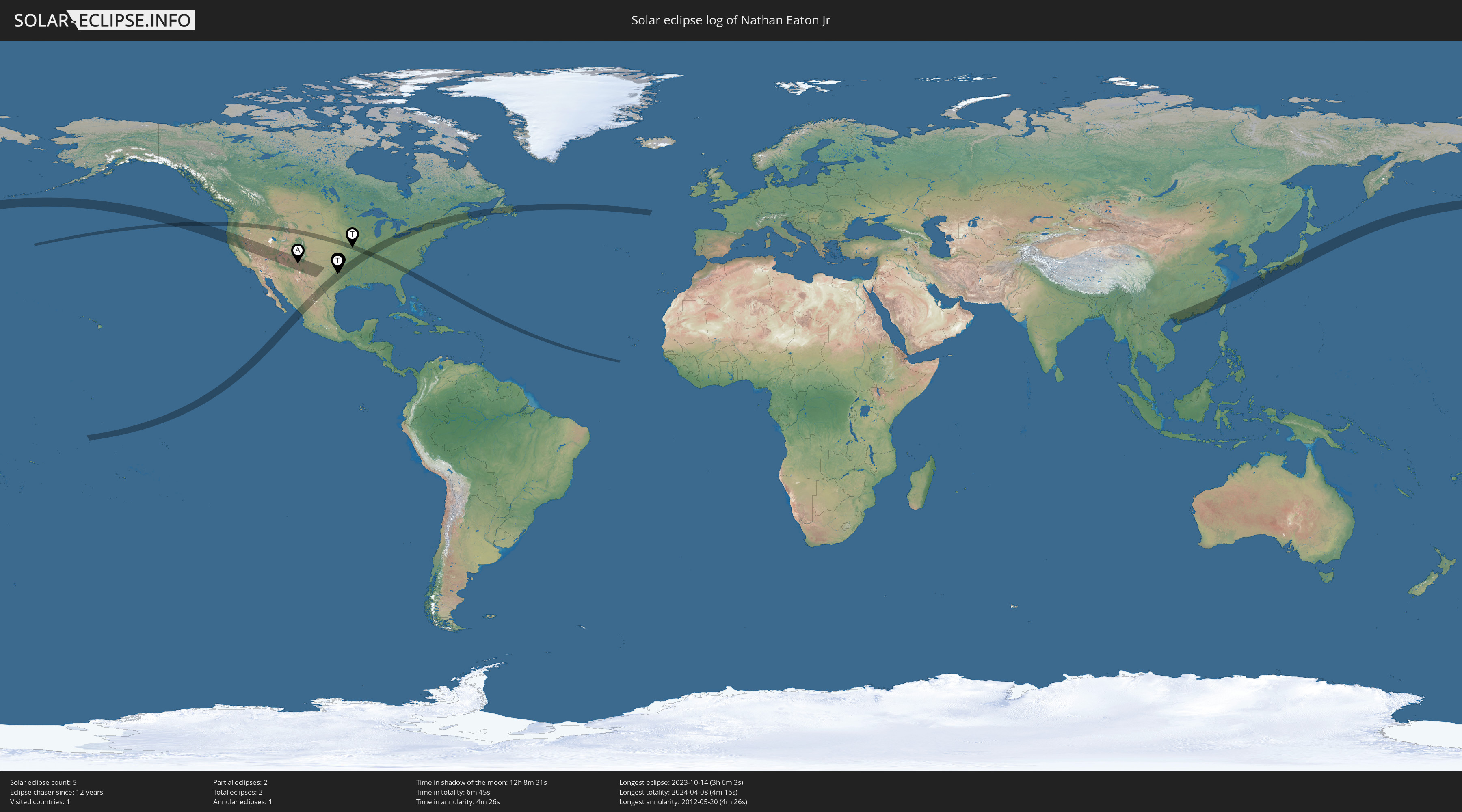
The first factor to consider is that the Sun and Moon are similar but not exactly the same size from our viewpoint. Actually, the distance to the Moon varies a little at different points in its orbit so sometimes it is closer and thus a bit larger than the Sun (necessary to have a total solar eclipse) and sometimes it is farther away and thus a bit smaller than the Sun (leading to views like the Ring of Fire of an annular eclipse such as the one on October 14th this year). But in general terms, they are both roughly a half a degree across viewed from Earth. That means if Brandon had captured a jet at 12,500 feet passing in front of the Sun instead of the Moon, his image would have looked similar, at least in terms of the relationship between the size of the jet and the size of the celestial orb it passed in front of. 

The second factor is that while I know the angular size of the sun (reported by Stellarium as 31.68 arc minutes at the time of my video), for me to determine things like the jet's altitude, I need to know the jet's angular dimension, too. 

To calculate this, I captured a single frame from my video, cropped and rotated it then used drafting software (FreeCAD) to measure the relative difference between the width of the jet's fuselage and the width of the Sun. The ratio came out to 55.25% which means the width of the jet body is 17.5 arc minutes. 

So, how did you do in high school or college trig class? I muddled through but that was also so long ago, I just don't recall the exact formula to use. Thanks to Google, though, it was pretty easy to find what I needed.

d = ( w / θ ) * 60

Simple, right? Well, except I'm missing one variable: w, or width. Google to the rescue again. If I assume that this jet was something like a Boing 737 or an Airbus 320, both pretty common models used by airline companies flying out of DFW and Love Field, then the width of the fuselage is approximately 13 feet. Plugging that into the formula as w and converting arc seconds to degrees and using that as θ, that tells me that the jet was approximately 2,674 feet away when it passed over our neighborhood. 

But was that how high it was flying? Not exactly since it wasn't directly over my backyard. Again checking Stellarium, I found that the Sun's altitude (its angle above the horizon) was about 62.65 degrees.

Dusting off more trigonometry, that gives me two variables of a right triangle, the angle and the hypotenuse. From those, I can calculate the jet's elevation (the opposite side of the triangle) and the distance over ground to the jet's position when it transited the Sun. 

o = h * sin(θ)

a = h * cosin(θ)

Solving these is pretty straightforward with a modern calculator or using spreadsheet software like Google Sheets. Note that these formulas require the angle to be expressed in radians but spreadsheets have a function for that, too, so you don't have to remember the formula for converting degrees to radians:

θ radians = θ degrees * π / 180

So what's the answer? Based on the numbers above, at the time it passed in front of the Sun that jet was flying at an elevation of approximately 2,377 feet and its position over land was about 1,225 feet from my backyard, about a quarter of a mile to the southwest.

I would have thought the jets flying over East Dallas would be higher than that but the data and formulas say it has to be somewhere between 2,000 and 3,000 feet up. To see for yourself, make a copy of my spreadsheet and play around with what happens when you change the jet fuselage width (cell B7). Even if you change it to the size of a jumbo 747, 21.3 feet, the calculated elevation of the jet is still well under 4,000 feet.

Another interesting exercise would be to play around with the ratio of the jet fuselage width to the orb size to see what it has to be for the jet in Brandon's image to be flying at 12,500. Give it a try.

Remind you of one of those math word problems you hated solving in school?

Yeah, but pretty cool, huh?

Note

It's been decades since I was in school so if you find that I've made a mistake in my calculations, I'd be happy to hear about it in the comments.

Solar Transit of a Jet

UPDATE: I've replaced the previous video with a new version that includes the sound of the jet flyover from the original audio track. 

While out filming the sun to practice for the total solar eclipse next April, I was photo-bombed by a jet! 

The technical term is "transit", when an object crosses in front of an astronomical body. There is plenty of air traffic over our house with Love Field and DFW serving the area so I guess this shouldn't have surprised me but observing a transit (like this one, or this one) takes being in just the right place at just the right time so it's a pretty rare thing to have happen. 

One reason I happened to be shooting at this time is that I'm working out exactly what equipment I'm going to be shooting with for the total solar eclipse. This video was shot using:

• Sky Watcher EvoStar 72ED refractor
• Baader film solar filter
• 2" mirror diagonal
• Celestron 1.25" 2X Barlow
• T2-ring
• Nikon D750 DSLR
• Focusing with DeepSkyDad AF3 autofocuser
• Sky Watcher Star Adventurer 2 tracker
• Radian carbon fiber tripod

I have a new 2" 2X Barlow and I plan to shoot straight-through (i.e., no diagonal) but I am still working out what combination of components will allow me to properly focus with the new Barlow. Once I have that worked out, I'll start working on automating my astrophotography workflow using a small computer (a Raspberry 4 running software called StellerMate).  

The quality of this video isn't great but that's basically because I was focusing (pun intended) more on getting the equipment working right than on the finer details. Next April may see a long ways off but it will be here in the blink of an eye and as I know from my experience in 2017, being ready to catch a full eclipse end-to-end, most importantly those few minutes of totality, takes an incredible amount of practice. So, I'll be shooting pretty regularly over the next few months to make sure I have everything working perfectly. 

Anyone have a way to ensure that April clouds don't spoil the eclipse for me, er, us?

Seriously, you'll notice from the video that the Sun is pretty active with quite a few sunspots showing. Over the next few weeks, if I can get a day with good "seeing" (i.e., where there is minimal air turbulence), I'll get some shots with lots of detail, everything in focus, and the sunspots should jump off the page at you. Stay tuned!

Warning 

NEVER look directly at the sun without proper protection. This video was shot using a telescope and camera equipped with a special solar filter.

Blue Moon Rising Over White Rock Lake

With the extreme Texas heat, lately I've been waiting till after sunset to take our Weimaraner, Luna, for a walk and we've been walking along the shore of White Rock Lake near where we live since it's often cooler with a little breeze coming off the water. 

I had not planned to shoot the Blue Moon tonight, but after my wife Linda asked if I would be, it occurred to me that it would be visible over the eastern shore of the lake when Luna and I were out walking. I decided to see if I could get a shot of the full Moon rising over the sailboats at Corinthian Sailing Club before our walk. I grabbed my small refractor (Sky Watcher EvoStar 72ED), my Nikon D750 and a tripod, loaded Luna in the car and headed to the lake. 

Apparently, so did everyone else. I guess the news of the Blue Super Moon got enough press that lots of other people showed up at the lake to watch it rise and traffic driving up the west shore was like rush hour. By the time I was parking the Moon was already well above the tree line. I hastily set up the scope and camera, got a reasonably good focus on the Moon and started shooting. All the while, Luna hung out with me, thankfully only wrapping her lead around the tripod as I was finishing up. 

Ironically, the shot below was the first shot I took. Of all the others, I could perhaps merge a few bracketed shots for something with a higher dynamic range but frankly this is pretty much the shot I had in mind when I left the house. 

Enjoy!

As always, click on the image to see full-screen. 

2023 Perseids and Mesquite Tree

In the wee hours of this morning, my mother Doris' birthday, I drove out east of Dallas looking for dark(er) skies to view and capture the 2023 Perseid meteor shower. The first spot I had planned to try turned out to have more brightness in the sky than I hoped for so I went a little farther out and found a quiet spot on a country road in College Mound just southeast of Terrell. Parking well off the road in front of a pasture gate, I set up two cameras shooting east across the pasture with a mesquite tree in the foreground. I'm still going through all the images and may eventually post a composite similar to the one I did in 2016 but this image has the best and brightest of the ones I captured. 

This was taken with a Nikon D750 using an Irix Firefly 15mm f/2.4 wide angle lens. It's a 20 second exposure taken at f/2.8 and IS) 6400. I processed it in Lightroom to adjust brightness, contrast and color temperature. 

Not an ideal composition given the streaking speck of comet dust is right at the edge of the frame and cut off midflight but it's still a beauty. And it's not alone. Besides the Pleiades and Jupiter, look close and you'll find at least one other Perseid and at least one satellite. Even with the comparatively dark Bortle 4.5 class skies, there are still light domes on the horizon from towns further east like Wills Point to the left. The yellowish glow towards the center is from the rising crescent moon not yet visible above the treeline.

I'll share more once I have time to go through the rest of the images from both cameras. In the meantime, enjoy!

Click the image to enlarge. 

Olivia and Papa Chase the ISS and More

Last month, my granddaughter Harper and I went out to capture an image of the International Space Station (ISS) flying over Dallas. As described in my post about that effort, we were only partially successful, foiled by clouds. This past Tuesday evening, granddaughter Olivia and I headed up to the north shore of White Rock Lake to try again. In spite of being a little late getting to the lake and rushing to set up cameras, we managed to catch the last 90 seconds or so of the ISS flyover as it traveled from the northwest, overhead and down to the southeast. Here is the result.

This is a composite image created by stacking 9 images taken with a Nikon D750 and a Rokinon 14mm wide angle lens mounted on a tripod. Each shot was 8 seconds long with 2 seconds between each shot. What Olivia and I saw was an incredibly bright "star" moving across the sky, too steady and too fast to be an airplane. It appears as a streak in this image due to the long exposure of each original image; the gaps are due to the delay between each shot while the camera saved the image files. 

This photo demonstrates an interesting aspect of ISS flyovers. We can see the ISS fly by only at certain times and places, its visibility due to the viewer being in a position to see sunlight reflected off of the ISS. For this flyover, as it was traveling "away" from the sun (which had set just over an hour earlier) its orbit carried it into the Earth's shadow. Notice how the lowest trail fades off and disappears. 

Another interesting object in the sky that night was the Sturgeon Moon, the first of two "supermoons" this month. It was cloaked in clouds until just as we were getting in the car to head home so it just appears in this image as a bright glow to the lower left. Note all the people on the dock though; there was quite a crowd out that night with people all up and down the shoreline to watch the full moon rising. I wonder how many of them also realized they were getting a chance to see the ISS, too.

We also tried to capture a flyover of a satellite, BlueWalker 3, which passed over this same view looking south across the lake about a half-hour before the ISS flyover. Unfortunately, even having two cameras shooting during its flyover, we didn't capture it. I'm not sure whether it was due to its lower elevation, the haze to the south east or a miscalculation on my part about where and when we would see it. That'll be a target to try for another night. 

Thanks to the long exposures taken, the composite includes more than just the ISS and the Moon. Stars of the constellation Sagittarius (the Archer) and Scorpio (the Scorpion) are visible including Antares, the red super-giant star that is known as the Heart of the Scorpion. Here is a labeled version of the image above. 

The images above were edited to remove all the other stuff we saw in the sky that night: aircraft. The following is a composite of 12 images stacked "as is" in Photoshop. It shows not only the ISS but all the aircraft trails captured. Having simply stacked the images, stars appear as streaks and headlights and taillights of cars on the far shore of the lake appear as streaks. 

One final image, this time an edited stack of all the images, showing not only the ISS but all the aircraft trails captured. Unlike the unedited stack, in this view the sky (Moon and stars), lake and even the car headlights on the far shore are all from a single image. The aircraft and ISS trails from the other 11 images were masked to overlay that single image.

As always, click on an image to see large.